Note
MSE = bias$^2$ + variance
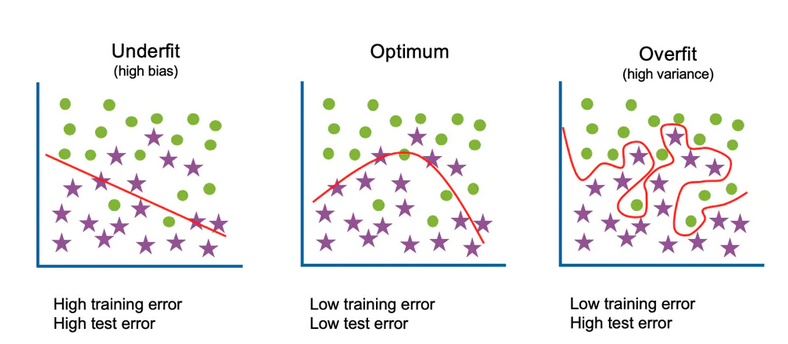image source: https://www.codingninjas.com/codestudio/library/bias-variance-tradeoff
Bias (Underfitting)
$$Bias[Y_{pred}|Y_{true}] = E[Y_{pred}] - Y_{true}$$ the **bias** error is an error from incorrect assumption in the learning algorithm. high bias can cause an algorithm to miss the relevant relations between features and target output (**underfitting**) (systematic off-the mark)
Variance (Overfitting)
$$ Var[Y_{pred}|Y_{true}] = E[(Y_{pred} - Y_{true})^2] - E[Y_{pred} - Y_{true}]^2$$
the variance is an error from sensitivity of the training data. high variance may result from the algorithm model noise from the training data (overfitting)
Avoid Overfitting
- early stopping
- train with more clean data
- data augmentation: sometimes adding some noise can stabilize the model
- feature selection
- regularization
- ensemble method
important additional read: https://arxiv.org/pdf/1812.11118.pdf
MSE
$$MSE = E[(Y_{pred} - Y_{true})^2]$$
$$MSE = (E[Y_{pred}] - Y_{true})^2 + (E[(Y_{pred} - Y_{true})^2] - E[Y_{pred} - Y_{true}])$$ $$MSE = Var[Y_{pred}|Y_{true}] + E[Y_{pred} - Y_{true}]^2$$ since $Y_{true}$ constant: $$MSE = Var[Y_{pred}|Y_{true}] + (E[Y_{pred}] - Y_{true})^2$$ $$MSE = Var[Y_{pred}|Y_{true}] + Bias[Y_{pred}|Y_{true}]^2$$