mapping outcomes -> numbers from a random process

Discrete

Suppose X is a discrete event, we denote probability of $X=x$ by $p(X=x)$, or just $p(x)$ for short. Here $p(x)$ is called a probability mass function or pmf.

Continuous

Suppose X is some uncertain continuous quantity. The probability that X lies in any interval $a \leq X \leq b$ can be computed as follows:

1. define event $A = (X \leq a)$, $B = (X \leq b)$, $W = (a < X \leq b)$
2. we have that $B = A \lor W$ and since A and W are mutually exclusive, the sum rules gives:
3. $P(B) = p(A) + p(W)$ hence $p(W) = p(B) - p(A)$

Define the function $F(q) \triangleq p(X \leq q)$. This is called the cumulative distribution function or cdf of X. Using this notation we have: $$p(a < X \leq b) = F(b) - F(a)$$ now define $f(x) = \frac{d}{dx}F(x)$ this is called the probability density function or pdf. Given a pdf now we can compute probability of a continuous variable being in a finite interval as follows: $$P(a < X \leq b) = \int_a^b f(x) dx$$

Transforming RV

Scaling/Shifting

if we shift the random variable X by k, the probability density function of p(X) will be shifted and the new mean will become: $\mu_x + k$ but the standar deviation will be the same

if we scale the random variable X by k both of the mean and std will be scaled by k

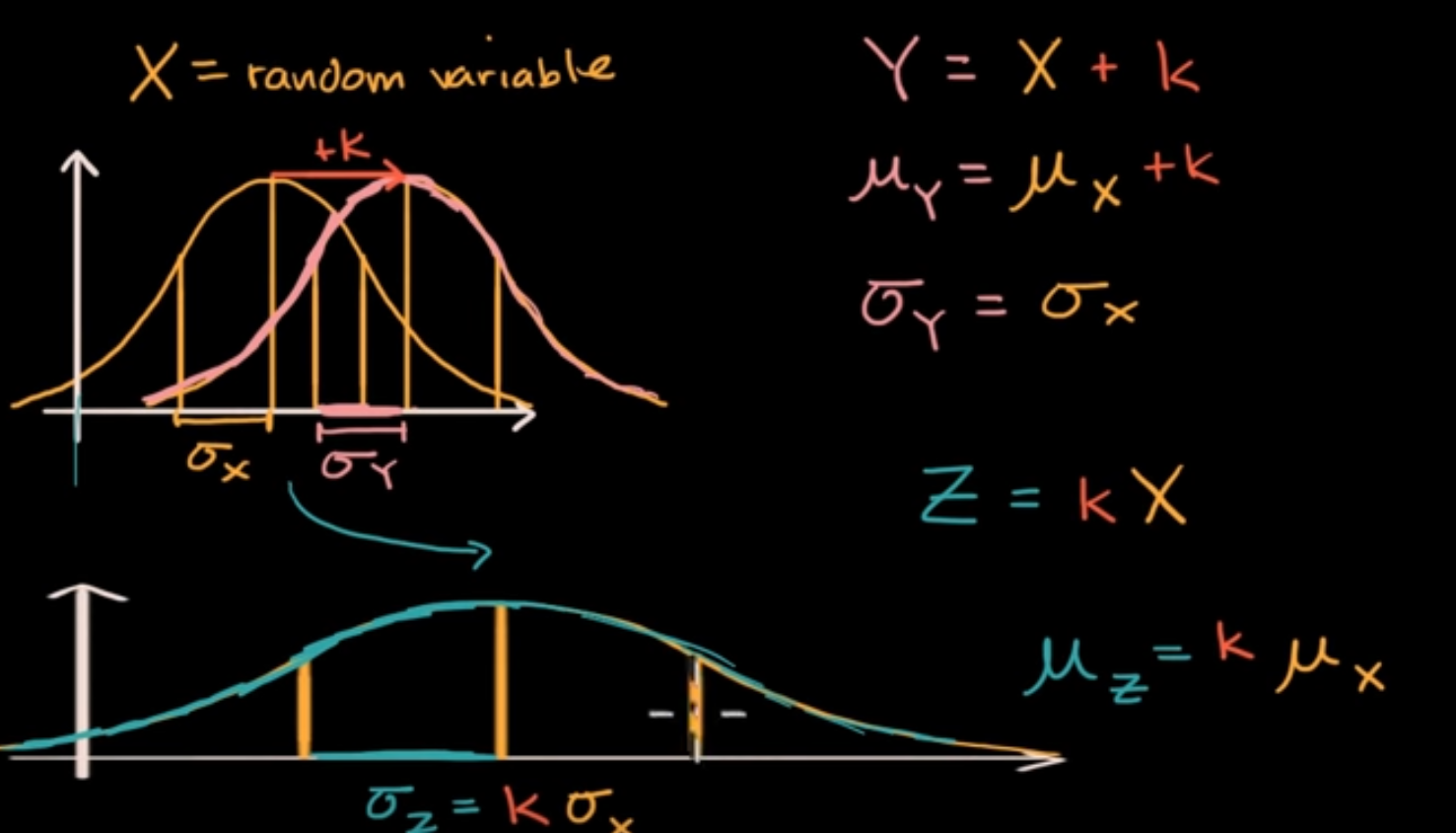image source: Khan academy

References

1. https://www.khanacademy.org/math/statistics-probability/random-variables-stats-library
2. page 28 and 32 of ML a probabilistic perspective by Murphy